对小学数学知识模块和具体知识点的整理

小学数学是学生初步学习数学学科的阶段，是打基础的阶段。随着社会科学的发展，小学数学涉及的内容也在不断变化。相对而言难度增加不少。与中学数学的衔接越来越紧密。所以学好小学数学是基础，也是关键。不仅是知识技能的掌握，也是数学思维能力和数学素养的培养。

小学数学涉及哪些知识模块

一、计算

数和数的运算是小学数学的基础。本模块包括整数、分数、小数、百分数的概念、相互转换、比较，加减乘除等基础运算。

具体： 1、四则混合运算与速算、巧算

2、等差数列的求和

3、比和比例的计算

4、估算和取整

二、几何图形和测量

几何图形和测量包括平面图形和立体图形的概念、分类、属性、构造、绘制及测量和计算的技能。

具体：1、平面图形的性质和运算

2、周长与面积

3、立体图形的表面积和体积

4、图形的变换与对称性

5、圆与圆的性质

三、代数的初步

代数在小学阶段的出现，是小学数学的拓展，不再是“算术”。主要涉及：等式的认知和建立及运用；用字母表示数；简单方程式的解法等。

四、数论

本模块包括自然数的性质，质数和合数，倍数和奇数（如何求最小公倍数和最大公约数）

五、计数

本模块涉及：

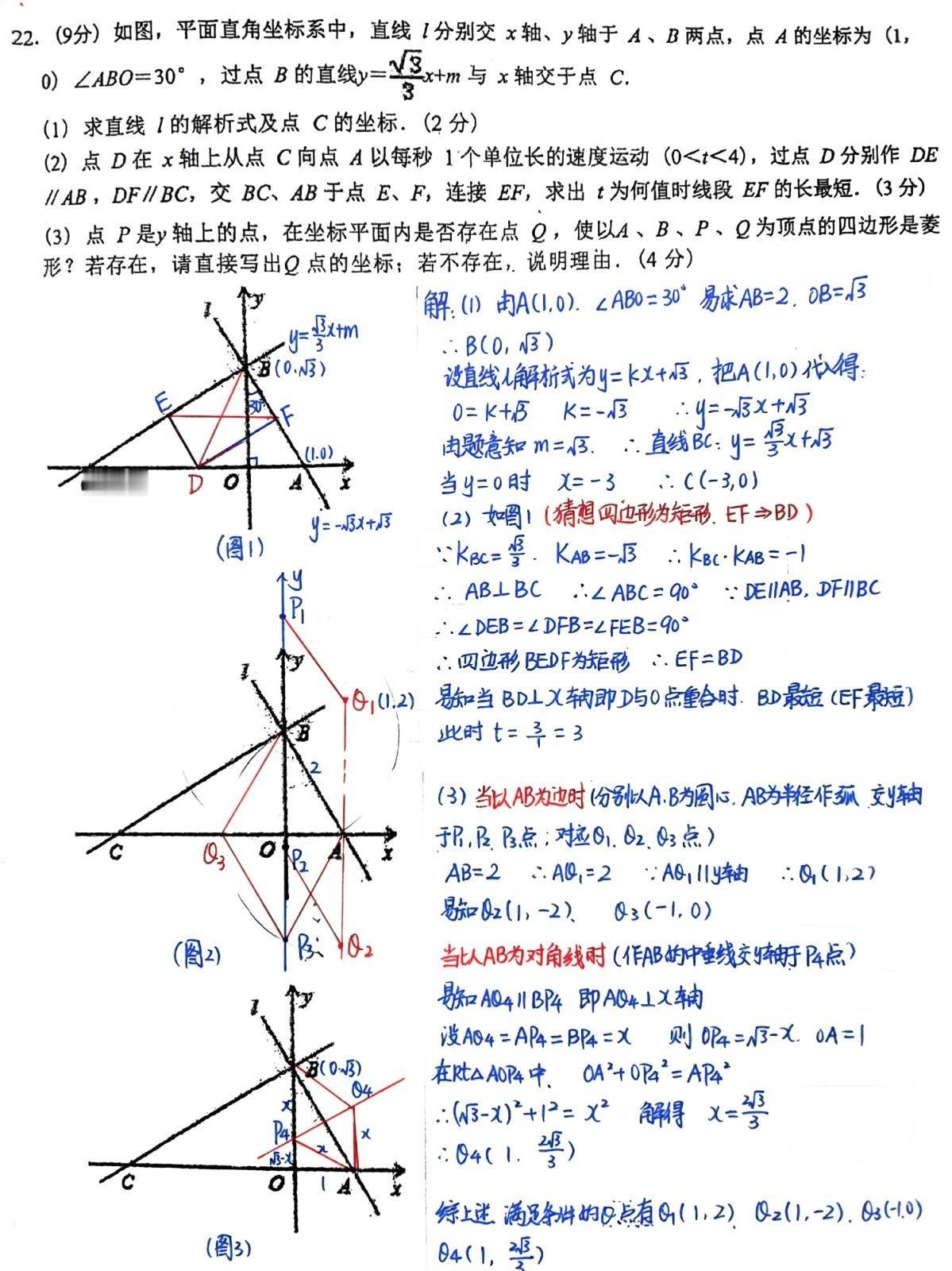
1、加法原理和乘法原理

2、排列与组合

3、列表与数阵

4、概率与统计

六、常见应用题（题型和解题方法）

算：

（1）速算和巧算

（2）等差数列：求和 =（首项+末项）×项数÷2

项数 =（末项-首项）÷公差+1

末项 = 首项+公差×（项数-1）

首项 = 末项-公差×（项数-1）

公差 =（末项-首项）÷（项数-1）

等差数列的奇数个数的和=  中间项×项数

（3）分数的计算（一般计算法和裂项求法）

（4）百分数的计算

（5）进位制的换算

（6）余数的求法

2、基础应用题型

（1）还原问题：怎么来的怎么回去（方法：倒推法）

（2）和差问题：已知两个数的和和差，求这个数的问题

大数=（和+差）÷2   小数=（和-差）÷2

（3）倍数问题：已知两个数的和（差）以及一个数与另一个数的倍数关系，求两个数的问题

和÷（倍数+1）=1倍量   差÷（倍数-1）=1倍量

（4）年龄问题：关键：两个人的年龄差是不变的

（5）  盈亏问题：已知两个分配方案，一次分配有余，一次分配不足，求人数。（还有其他类型：两盈，两亏、一亏一尽、一盈一尽）

解法：两次结果差÷两次分配差=人数

（6）植树问题：植树线路是不封闭的三种情况和植树线路是封闭

株数=路长÷株距+1

路长=株距×（株数-1）

株距=路长÷（株数-1）

（7）鸡兔同笼问题：解题方法：1、假设法 2、打包法  3、抬脚法

这里讲解的是一般应用的方法：假设法。（视频里有其他方法）

假设都是兔子或鸡的时候，出现了脚比实际脚数多或少，从而解题

兔子=（实际脚数-每只鸡脚数×鸡兔总数）÷（每只兔子脚数-每只鸡脚数）

（8）归一问题：特点：先求一份是多少。归一问题可分正归一和反归一。在求一份是多少后再求几份是多少  ——正归一。反之为反归一

解决归一问题的关键是求出一份的量：总数÷份数=一份量

（9） 归总问题：先求出总数，再根据问题的要求，求出每份是多少？或有这样的几份？

计算方法：每份数×份数=总数

（10）行程问题（相遇问题、追及问题、流水问题)

相遇问题：相向而行。                       相遇距离=速度和×相遇时间

追及问题：追及距离=速度差×追及时间

流水问题：逆水速度=船速-水速   顺水速度=船速+水速

（11）工程问题：当我们完成一项任务，常常需要计算有关：工作总量、工作效率、工作时间的问题，叫工程问题。

工程问题的特点：题目中的工作总量一般不是具体的数，而是单位1来表示，工作效率以时间单位内完成工作总量的几分之几来表示。

三者关系：工作总量÷工作效率=工作时间（不变）

（12）浓度问题：糖与糖水重量的比值叫做糖水的浓度，盐与盐水重量的比值叫做盐水的浓度。药与药水重量的比值叫做药水的浓度。

一般关系量：溶液重量、容质重量、溶剂重量、浓度（浓度是个百分比）

溶液重量=溶剂重量+溶质重量

浓度=溶质重量÷溶液重量

溶质重量=溶液重量×浓度

溶液重量=溶质重量÷浓度

溶剂重量=溶液重量×（1-浓度）

（13）分数和百分数一般应用题

1.1  求一个数的几分之几（或百分之几）是多少？

解：这个数（表示单位1的量）×分率=分率对应的量

1.2  已知一个数的几分之几（或百分之几）是多少，求这个数？

解：分率对应的量÷分率=这个数

（14） 比和比例

1    关于比的意义和性质

两个数相除又叫做两个数的比，a÷b(b≠0)可记做：

a(前项）：（比号）b（后项）

a:b=a n:b n(n≠0)

a:b:c=a n:b n:c n(n≠0））连比

2      正比例和反比例

表示两个比相等的式子叫比例  a:b=c:d  (b≠0.d≠0)         a,d叫外项，b,c叫内项，

正比例：两个相关的量，一种量变化，另一种量也随着变化，它们的比值是定值。叫正比例   =k

反比例：X  ×  y = k (一定）

（15） 方阵问题

在日常生活种，我们会遇到和方阵问题相关的实际问题：如编排、摆设等。方阵有两种：一种空心方阵，一种实习方阵。我们可以看图理解。

A:（3X3的实心方阵）   B  3x3的空心方阵

方阵的特点：

都按正方形排列

同一层内每边的个数相等

每向里一层，每边的个数少2

实心方阵：总个数=外层每边的个数×外层每边的个数

空心方阵：总个数=（外层每边个数-层数）×层数×4

（16）抽屉原理

有m件物体，放进n个抽屉，如果物体比抽屉数多，那么比然一个抽屉要放两个及两个以上的物体。

（17） 格点和面积

这是一种特殊的计算图形面积的方法。

公式：L/2 -(S-N)=1   （L 表示图形边缘上的点  ； S表示图形的面积  N表示图形内部的格点），这个公式不是对所以的多边形都成立。

（18）一笔画

能一笔画的图形的特征：图形中奇点个数必须为0或者2；如果图形只有偶点构成必定可以一笔画。

（19）利润和折扣问题：基本关系量

1  利润率=（售价-成本）÷成本×100%

1.2   售价=成本×（1+利润率）

1.3  现价=原价×折扣

4   定价=成本×（1+期望利润率）

关于数论的一些知识点

1、倍数与约数：如果一个自然数a被另一个自然是b除，余数为零，那么我们说a能被b整除。a是b的倍数，b是a的因数（约数）

（1）如果一个数的个位数字是0、2、4、6、或8，那么2是这个数的约数。即：能被2整除的数的特征。

（2）如果一个数的各个位置上的数字和能被3（9）整除，那么这个数也能被3（9）整除。

（3）如果一个数的个位数字是0或5，那么这个数能被5整除。

（4）如果一个数的末三位数字组成的数，与末三位以前的数字所成的数，它们的差能被7、11、13整除，那么这个数也能被7、11、13整除。

（5）如果一个数奇数位上的数字和偶数位上的数字和相减的差能被11整除，那么这个数能被11整除。

相关的规律还有，但要灵活，适当的运用在计算中，才能起速算的效果。

2、质数和合数是很重要的两类数。简单说：如果一个数的约数只有1和它本身，那么这样的数叫质数（素数）；如果一个数的约数除了1和本身外还有其他的数，那么我们称之为合数。

把一个合数用质因数相乘的形式表示出来叫分解质因数。（我们可以用短除法）

一般地，若n个质因数分解为：paqb……那么n就有（a+1)(b+1)……个约数。

3、最小公倍数和最大公约数：辗转相除法。

4、奇数和偶数：一般说：能被2整除的数叫偶数，不能被2整除的数叫奇数。0是偶数。

5、余数和同余：我们在运算除法时，往往会出现除不尽，那么就会有余数，对余数的研究有十分重要的意义。

（1）一般地，对于任意的两个自然数a,b，都有整数q（商），r(余数），使得：a=b×q+r  (0≦r≦b)

（2）同余的定义：已知两个整数a,b，及一个整数m，如果M I a-b，就称a,b对应模m同余，

记作：a≡b(mod m）

（3）关于进位制的互化。

十进制和二进制的 转换

二、小学几何知识

1、线段、射线、直线：这是构成平面图形的基本元素。线段有两个端点，射线有一个端点并向一个方向无限延伸，直线则向两个方向无限延伸。

2、角：由两条射线共有的公共端点组成。角的大小与两边叉开的大小有关，与边的长短无关。角的大小通常以度（°）为单位进行测量。

3、三角形：由三条线段围成的图形，是最简单的多边形。三角形的内角和等于180度，并且任意两边之和大于第三边。

4、四边形：由四条边围成的图形，包括平行四边形、长方形、正方形和梯形等特殊类型。

5、圆：一种曲线图形，圆上的任意一点到圆心的距离都相等，这个距离称为半径。

6、轴对称图形：沿一条直线对折后，直线两侧的部分能够完全重合的图形。

7、周长：围成一个图形的所有边长的总和。

8、面积：表示一个平面图形的大小，通常以平方单位表示。

圆和圆的性质

1、圆的定义

在一个平面内，一动点以一定点为中心，以一定长度为距离旋转一周所形成的封闭曲线叫做圆。圆的中心叫圆心，用O表示。连接圆心和圆上的任意一点的线段叫做半径，字母表示为r；通过圆心并且两端都在圆上的线段叫做直径，字母表示为d。在同一个圆中，圆的直径= d    d=2r 。

2、圆的基本性质

对称性

1、圆是轴对称图形，其对称轴是任意一条通过圆心的直线，圆有无数条对称轴。圆也是中心对称图形，其对称中心是圆心 。

2、垂径定理及其推论：垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的弧。

推论：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的弧；弦的垂直平分线经过圆心，并且平分弦所对的两条弧；平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧；圆的两条平行弦所夹的弧相等 1345。

3、圆周角与圆心角性质

（1）圆心角：顶点在圆心上的角叫做圆心角。

(2) 圆周角：顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角。

（3）圆周角定理：相同弧所对的圆周角等于圆心角的一半；在同圆或等圆中，同弧或等弧所对的圆周角相等；同圆或等圆中，相等的圆周角所对的弧也相等。

(4)特殊情况：直径所对的圆周角是直角，90度的圆周角所对的弦是直径 1235。

4、弧、弦和弦心距关系

5、在同圆或等圆中，相等的弧所对的弦相等，所对的弦的弦心距相等

6、外接圆和内切圆性质

外接圆：一个三角形有唯一确定的外接圆，外接圆圆心是三角形各边垂直平分线的交点，到三角形三个顶点距离相等。

内切圆：一个三角形有唯一确定的内切圆，内切圆的圆心是三角形各内角平分线的交点，到三角形三边距离相等，内切圆半径=R=2S△÷L（S △为三角形面积，L为三角形周长）。

7、相切性质：两相切圆的连心线过切点；如果两圆相交，那么连接两圆圆心的线段（直线也可）垂直平分公共弦

8、其他角度性质

弦切角的度数等于它所夹的弧的度数的一半。

圆内角的度数等于这个角所对的弧的度数之和的一半。

圆外角的度数等于这个角所截两段弧的度数之差的一半

9、面积性质

周长相等时，圆面积比正方形、长方形、三角形的面积大

10、圆和圆的位置关系

位置关系分类

外离：两圆无公共点，一圆在另一圆之外。

内含：两圆无公共点，一圆在另一圆之内，特殊情况为两圆是同心圆（圆心距=0   d=0）。

外切：两圆有唯一公共点，一圆在另一圆之外。

内切：两圆有唯一公共点，一圆在另一圆之内。

相交：两圆有两个公共点

排列和组合

排列：A(n,m)=n×(n−1)×(n−2)×…×(n−m+1)=n!/(n−m)!

组合；C(n,m)=A(n,m)/m!=n!/m!(n−m)!

加法原理：做一件事情，完成它有N类方式，第一类方式有M1种方法，第二类方式有M2种方法，……，第N类方式有M（N）种方法，那么完成这件事情共有M1+M2+……+M（N）种方法。

乘法原理：乘法原理是指完成一件事需要分成n个步骤，每个步骤有不同的方法数，那么完成这件事总共的方法数是各步骤方法数的乘积。

概率统计和排列组合是比较难的，小学阶段还没有到这样的教学要求。是通过实际的例子，进行学习。如：搭配问题，乘车有几种方法等，重在培养孩子的思维能力。

小学数学虽然是数学学习的启蒙和基础，但所学的知识模块已经提高了不少的要求，渗透了初中，高中的知识，所以在学习的过程中以计算和计算能力为主的同时，要学习的知识点还有很多。从易到难，循序渐进地扎扎实实地学好，学透。不懂的地方一定要弄懂！正所谓万丈高楼平地起。