:是描述占据概率的核心参数,绝对零度时为占据态与非占据态分界,有限温度下遵循费米狄拉克分布,等同于。其在中决定类型,金属中位于导带,是连接微观电子结构与宏观性质的桥梁。
泛函计算费米能级是量子统计力学中描述费米子(如电子)能态占据概率的核心参数,其物理意义与统计分布特性共同构成了理解固体电子结构与宏观性质的基础。
从核心定义来看,在绝对零度时,E_F)是电子占据态与非占据态DOI:10.1016/j.rinp.2025.108158
E_F该分布函数表明,E_F是电子占据概率恰好为50%的能量点——当E远低于E_F时,f (E)≈1(几乎被占据);当E远高于E_F时,f (E)≈0(几乎空着);而在E≈E_F附近,占据概率随能量变化平缓过渡,这一特性直接决定了材料的电学、热学等宏观性质。
从物理本质来看,义:其一,它标示了能带填充的极限,在半导体中,费米能级的位置是决定载流子类型与浓度的关键因素。对于型半导体,掺杂引入的施主杂质会向导带提供电子,使费米能级向导带底靠近,此时导带中的电子浓度可通过积分导带态密度与费对于,受主杂质会在价带中产生空穴,使费米能级向价带顶移动,此时空穴成为主导载流子。
DOI:10.1016/j.jallcom.2025.179318
的费米能级则呈现出独特的特性。金属的费米能级位于导带内部,此时导带与价带重叠,费米能级处的态密度不为零,这意味着存在大量处于费米能级附近的电子,这些电子可在外电场作用下自由移动,使金属具有良好的导电性。
7.0 eV半金属的费米能级则位于附近,此时费米能级处的态密度较低,但能带交叉形成的线性色散关系会产生高迁移率的狄拉克费米子,使其表现出独特的输运性质——如石墨烯的费米能级可通过栅压调控,当费米能级位于狄拉克点时,电导率呈现极小值,而偏离狄拉克点时电导率随载流子浓度线性增加。
DOI:10.1002/adfm.202102275
怎么算费米能级?
(DFT)为核心,结合交换关联泛函的改进与迭代算法的优化,实现对不同材料体系的精准计算。
DFT,费米能级通过总能量对电子数的导数定义,这一定义直接关联电子化学势,表明费米能级是系统电子“化学势能” 的量化指标。
密度矩阵E_iDOI:10.1016/j.jpcs.2025.112898
对费米能级计算精度的提升起到了关键作用。早期的局域密度近似()假设交换关联能仅依赖于局域电子密度,忽略了电子密度梯度的影响,导致在非均匀体系中费米能级计算偏差较大——例如,LDA计算的金属表面费米能级与实验值的偏差可达0.5 eV以上。
的出现显著改善了这一问题,其中Perdew-Burke-Ernzerhof(PBE)泛函通过引入电子密度的梯度修正,更好地描述了电子密度的空间变化,使非均匀体系的费米能级计算精度提升约30%,尤其适用于半导体、合金等电子分布不均匀的材料。
的体系,通过混合一定比例的精确交换能与GGA交换关联能,有效解决了传统DFT对带隙的低估问题,进而提升费米能级位置的准确性。
DOI:10.1016/j.physb.2015.08.015
迭代计算流程Kohn-Sham这一流程的核心在于通过自洽迭代平衡电子数与费米能级的关系,确保计算结果满足电荷中性条件,对于复杂体系,还需考虑电荷转移对电子密度的影响,通过引入泊松方程耦合电子密度与静电势,进一步优化费米能级的计算精度。
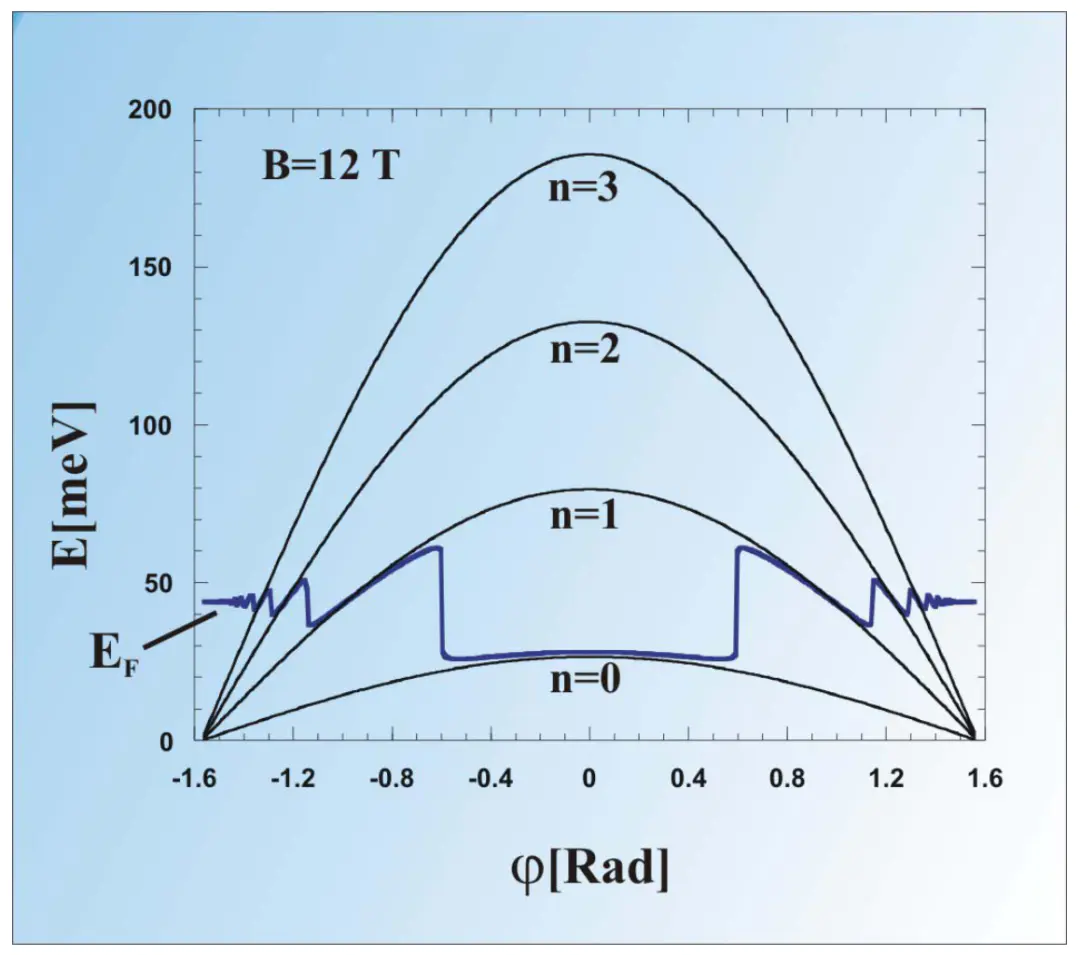
费米能级的应用贯穿于固体电子结构解析、输运性质预测及缺陷行为研究等多个领域,其数值与位置的精准确定为理解材料宏观性质提供了微观依据。
能带结构与费米面标注以拓扑半金属为例,通过微调费米能级使其向导带偏移60 meV,成功使计算的费米面与角分辨光电子谱实验结果匹配——图中费米面由E=E_F的等能面定义,色标表示对数尺度的谱函数强度,费米面的形状与拓扑结构直接反映了拓扑表面态的存在,而费米能级的微小调整即可显著改善理论与实验的吻合度,这一案例证实了费米能级位置对拓扑表面态预测的决定性作用,为拓扑半金属的器件应用提供了关键理论支撑。
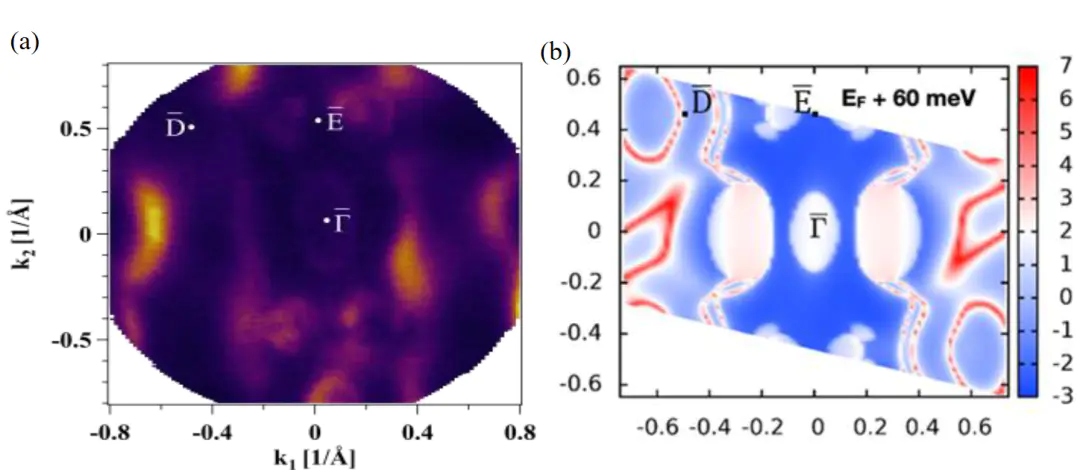
费米能级对输运参数的调控作用在中尤为显著。年关于分子导线电导衰减的研究表明,衰减常数(β)——描述电导随分子长度增加的衰减速率——对费米能级(E_F)具有强烈依赖性。
这一现象的物理本质是:费米能级与的相对位置决定了电子隧穿的概率——当E_F靠近HOMO或LUMO时,电子隧穿路径增多,衰减常数减小;而当E_F位于能隙中心时,隧穿概率最低,衰减常数最大,与实验观测一致。
DOI:10.1021/acs.jpcc.5b08877
缺陷形成能的研究Ge曲线的交点称为缺陷转变能级,即当跨越该能级时,缺陷的主导电荷态发生改变——例如,当E_F低于某一跃迁能级时,缺陷以-1价稳定存在;当E_F高于该能级时,缺陷则以0价更稳定。
费米能级通过计算不同E_F下的形成能,可预测缺陷在材料中的稳定电荷态及对载流子的影响,为半导体掺杂优化提供理论依据。
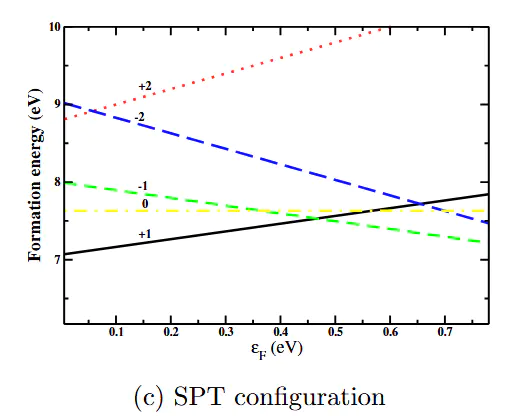
费米能级的E_F实现对材料新奇物理性质的发掘与应用。
在EuMnBi₂作为一种典型的狄拉克半金属,其费米能级可通过Gd³⁺掺杂实现有效移动:Gd³⁺的引入会通过磁理论计算揭示,这一现象源于狄拉克点附近的线性色散关系使载流子具有极高的迁移率,而E_F靠近狄拉克点时,参与输运的狄拉克费米子数量显著增加,导致Nernst效应大幅增强。
DOI:10.1002/adfm.202102275
二维半导体激子态演化MoS₂这一现象的物理机制是:E_F上升意味着导带中自由电子浓度增加,自由电子与激子的库仑相互作用增强,导致激子结合能增大;同时,带负电的三子与自由电子的屏蔽效应减弱,其结合能减小。
DOI:10.1103/PhysRevB.102.085304
揭示了尺度效应对电子结构的独特影响。计算表明,当银膜厚度从1 nm增至5 nm时,费米能级与膜厚呈线性关系,E_F随厚度增加而线性降低。
这一发现为纳米尺度金属器件的设计提供了关键参数:通过控制超薄金属膜的厚度,可调控其费米能级,进而优化器件的功函数、电导等特性,例如在纳米间隙器件中,通过厚度调控E_F可实现对隧道结电阻的精准控制。

费米能级作为理论计算与材料物理中的核心物理量,兼具物理本质与计算工具的双重角色,其精准描述与调控是理解材料性质、设计功能材料的关键。
费米能级定义了电子的统计分布规律与能带填充边界50%这一特性使其成为连接微观电子结构与宏观性质的桥梁:金属因费米能级位于导带内而具有高导电性,半导体的载流子类型与浓度由费米能级位置决定,拓扑半金属的独特输运性质则源于费米能级附近的线性色散能带。
。
从材料设计的角度来看,费米能级是性能调控的核心抓手。通过掺杂、电场、尺度控制等手段,可实现费米能级的定向移动,进而优化材料的光电、热电、输运等性能。
费米能级在“结构–性能” 关系中的核心地位,为新型功能材料的理性设计提供了明确的理论指导。随着计