人类文明经过数万年的发展，今天的数学体系已经变得无比地丰富与繁杂。

但是数学中有趣的故事，总是以最为简洁和优美的形式出现在数学王国的每一个角落。

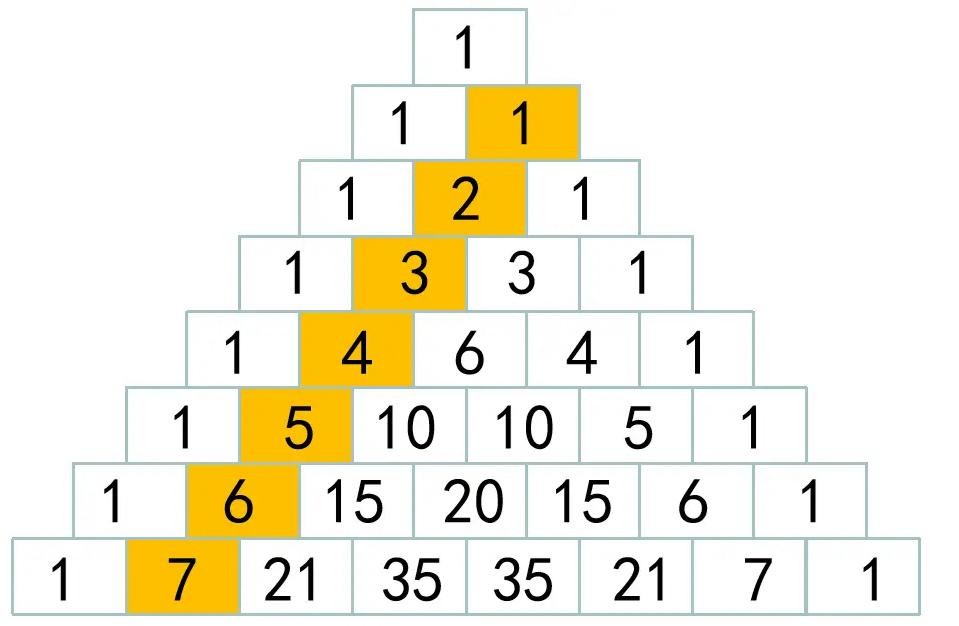
比如“杨辉三角”，这个在初中课本中出现过的小故事，却是流传于数学史上的不老传说。这到底是怎么回事呢？

还得从贾宪那本《黄帝九章算经细草》说起。

贾宪生于北宋，他撰写的这本书中记载了一个神秘的“三角图形”，这个图形名为“开方作法本源图”，也就是我们今天所说的“贾宪三角（即杨辉三角）”的核心。

有趣的是，在那个交通工具极不发达的遥远古代，在同时期的地球另一端的波斯学者卡拉吉，也不约而同地发现了这个神秘的三角。

虽然卡拉吉的工作与贾宪几乎处于同一时期甚至可能稍早，但贾宪最早给出了完整的图形和系统的方法。

这个三角在今天之所以被更广泛地称为“杨辉三角”，是因为贾宪的原著《黄帝九章算经细草》已经失传。

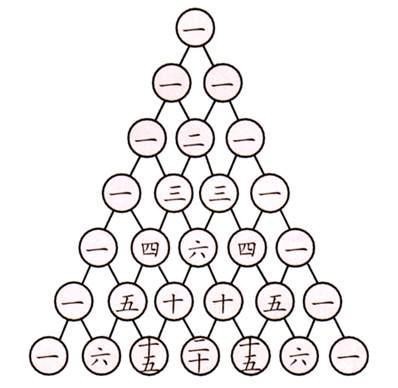
南宋末年的数学家杨辉，在他的著作《详解九章算法》中，收录并详细地解释了“开方作法本源图”，明代以后的学者，在学习这个三角时，读到的都是杨辉的书，所以人们称之为“杨辉三角”。杨辉在他的书中明确地说明了这个方法来自于贾宪。

“杨辉三角”为何有如此迷人的魅力？那是因为它的核心是“组合数”。

那么，“组合数”到底是怎么一回事呢？

“组合数”可以写成C（n，k），它的意思是从n个不同元素中任意取出 k 个元素的所有组合的个数。

如果我们规定杨辉三角的行数和列数都从0开始计数，那么第n行第k个数字的数值，恰好等于从n个不同元素中取出k个的组合数 C(n, k)。

“组合数”作为“组合数学”这一现代数学重要分支的基础，在概率论、统计学、计算机科学等诸多领域，甚至在群论、矩阵、微积分等领域都有它的身影。

第一，与“概率论”的关系

1655年，帕斯卡在一篇论文里提出并系统地探讨了这个三角的“组合数学”的性质，并且第一次与“概率论”进行了深刻的联系。

由于帕斯卡在西方的巨大影响力，所以在西方世界里，这个三角又称为“帕斯卡三角”。

在“组合数学”中，杨辉三角的第n行第k个数，正好等于从(n-1)个不同元素中取出(k-1)个的组合数，即 C(n-1, k-1)。

而在“概率论”中，比如抛4次硬币，得到2正2反的情况有6种（对应三角第5行的中间数6），概率是6/16。

第二，与微积分的关系

“杨辉三角”是二项式系数的一种“三角形”排列方式。

牛顿将“二项式定理”(a+b)^n的n扩展到“任意有理数指数”后，从而发展出“二项级数。

这一突破使得许多函数（如(1+x)^α）能够表示为幂级数，这为他后来系统地创立微积分学（特别是在函数的近似、求导和积分方面）提供了至关重要的代数工具。

在微积分中，莱布尼茨公式用于求两个“函数乘积”的 n 阶导数，而该公式的系数恰好对应“杨辉三角”的第 n 行，进一步体现了“二项式系数”在微积分中的直接应用。

18 世纪早期，数学家们在牛顿与莱布尼茨的基础上，开始探索“函数的级数”展开。

英国数学家泰勒于 1715 年发表《正的和反的增量方法》，提出“泰勒级数”。

在泰勒级数中，许多函数的“幂级数”展开会涉及“组合数”或“阶乘”，而“广义二项式定理”可视为“泰勒级数”的一个特例。二者均为更一般的“幂级数”展开理论中的特殊形式。

第三，与矩阵的关系

在“线性代数”中，“矩阵”是“离散数学”和“线性变换”的核心工具。

而数学中非常有趣的“帕斯卡矩阵”，它的元素直接取自“杨辉三角”。

在矩阵理论中，存在一种特殊的“帕斯卡矩阵”，其元素直接取自杨辉三角。通过研究这类矩阵，我们可以从“线性代数”的全新视角来理解和生成杨辉三角中的“组合序列”。

第四，与群论的关系

在群论中，所研究的是“对称性”和“抽象代数”结构。

在“对称群” Sn 的“表示理论”中，“不可约”表示的“维数”恰好等于将整数 n 拆分成“不同分拆”的“方法数”。而这些“分拆数”可以通过杨辉三角的某种“变体”或“推广”来研究和计算。

当我们在“素数 p 的模运算”下观察杨辉三角（即卢卡斯定理）时，它会呈现出规则的“分形结构”（谢尔宾斯基三角形）。这个结构深刻地联系着 “p-群”等代数概念。

第五、对未来的展望

直到今天，数学家们仍在挖掘杨辉三角的深层性质。

在量子力学中的“伊辛模型”中，每个粒子可以处于“向上”或“向下”态。在 n个粒子中，恰好有 k 个粒子向上的状态有多少个？答案就是组合数 C(n, k)，也就是“杨辉三角”第 n 行的第 k 个数字。

在弦理论中，“组合数学”和“二项式系数”作为数学基础的一部分，在将来，也许会在复杂的计算中作为结果出现。