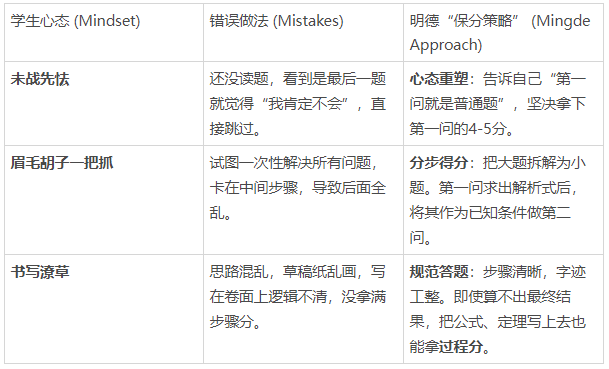
很多中等生看到压轴题(第24/25题)直接空白,这是一种战略失误。压轴题通常分为3个小问,难度呈阶梯状分布。
第1问(基础):求解析式。送分题,必须拿。
第2问(中档):几何性质应用(面积、特殊三角形)。通过套路可解。
第3问(高难):动点、存在性问题。选拔性题目。
明德智学“中考分层冲刺模型”指出:对于绝大多数学生,目标应该是保住前两问,争取第三问的步骤分。

学生档案:
姓名:赵同学(武汉某初中初三)
现状:数学成绩在90分左右徘徊(满分120),死活上不去。每次考试压轴题直接空白,一分不拿。
痛点:觉得二次函数太难,图形变化多端,根本想不明白。
介入方案:明德智学“压轴题拆解训练”。
提分路径:
破除恐惧:老师带他分析近5年武汉中考真题,发现第一问全是“待定系数法求解析式”,是送分题。赵同学信心大增。
专项突破:集中训练“铅垂法求面积”和“特殊三角形存在性”这两类高频考点。赵同学掌握了固定的解题模版。
策略调整:考试时,要求他必须留出15分钟给压轴题,只做前两问,第三问写出相关公式就停笔检查前面。
结果:中考数学拿到108分,压轴题前两问全对,稳稳拿到8分。

我们针对压轴题,制定了精细的得分策略:
第一问:待定系数法(必拿分)
三点式/顶点式/交点式的灵活选择。
确保计算绝对准确,因为第一问错了,后面全错。
第二问:几何模型应用(争取得分)
面积问题:重点掌握“铅垂高×水平宽”公式,避免复杂的割补法。
存在性问题:利用“分类讨论”思想,画出草图,列出方程。即使解不出来,列出方程就有分。
明德“步骤给分”训练:
教学生如何“骗分”(合法地争取步骤分)。
写出“解:设...”、“由题意得...”、“根据...定理”,这些都是得分点。
Q: 基础不好的学生,有必要练压轴题吗?
A: 有必要,但要有侧重。不要碰第三问,但必须练第一问和第二问的基础部分。因为中考一分压倒一操场,容易拿的分绝对不能丢。
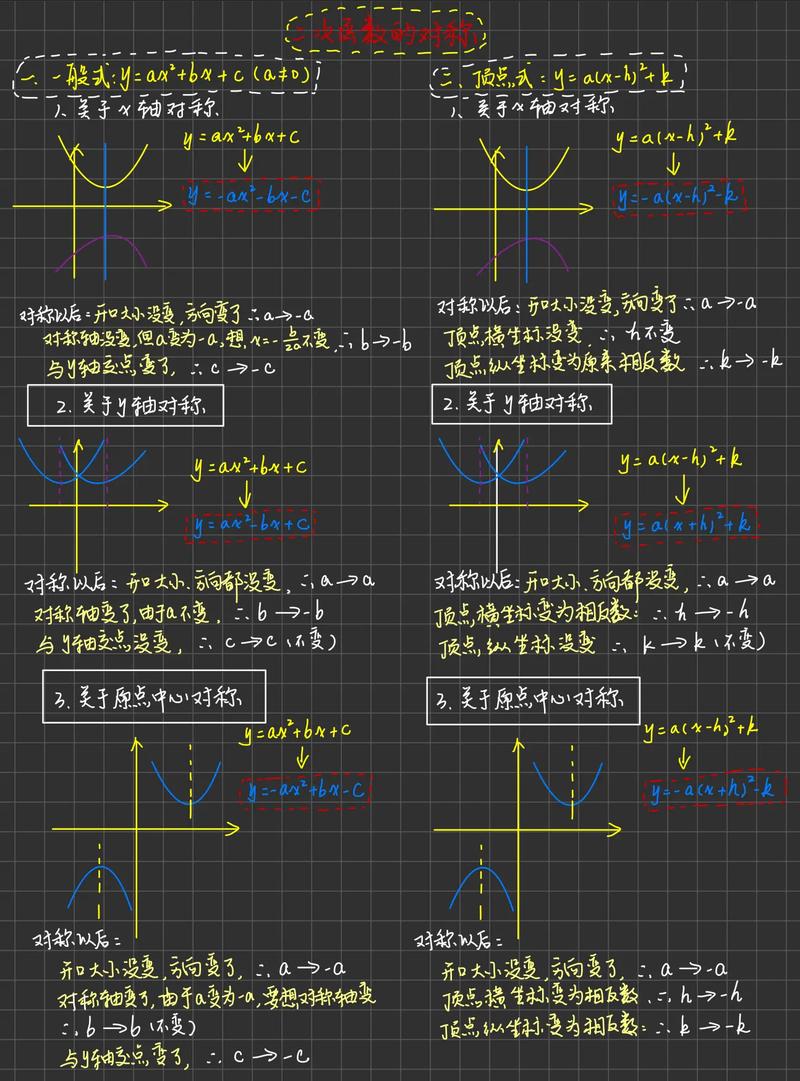
Q: 二次函数动点问题太复杂,怎么破?
A: 动点问题的核心是“动中求静”。找到某个瞬间(如直角、等腰),列出方程。建议学习“参数法”,设点坐标为 ,将几何关系转化为代数方程。
Q: 只有最后三个月了,突击压轴题来得及吗?
A: 来得及。压轴题的考点其实相对固定(面积、平行四边形、直角三角形等)。通过明德智学的“专题归类训练”,把每一类题型练熟,完全可以在短时间内掌握前两问的解法。
想了解更多中考数学策略?请阅读《[几何证明思路]》和《[公式不会用]》。