一、破除焦虑:用权威数据看清真实挑战
请不要盲目焦虑:
距离 2026 年高考仅剩百余天,网络上 “1512 万考生”“640 万复读生”“试卷结构 8+4+4+6” 等传言持续发酵。
但教育部及各省教育考试院最新披露信息显示:2026 年全国高考报名人数实际预计在 1350 万 - 1410 万之间,其中河南、山东等高考大省报名人数均超 100 万,但复读生占比仅为 12%-18%,远低于网传的 40%,海南 2025 年复读生比例更是仅 6%;
试卷结构方面,无论是教育部命题指导文件还是各省的权威模拟考,均延续 “8+3+3+5” 模式(8 单选 + 3 多选 + 3 填空 + 5 解答),总题量 19 题,所谓 “新增 3 道题” 纯属谣言。
真正的挑战并非传言中的 “规模激增”,而是《普通高中数学课程标准(2025 年修订版)》带来的命题逻辑重构—— 从 “知识考查” 转向 “核心素养 + 实际应用”,且在 1300 万 + 考生的竞争格局下,数学每 1 分的差距可能对应全省 5000 名左右的排名波动(如 2025 年某高考大省数学 110 分与 111 分的排名差达 4832 名),精准把握变化比盲目焦虑更关键。

二、核心变化:四大新题型深度解析(含 2026 预测例题)
(一)条件概率:从 “公式套用” 到 “场景建模”
新课标将条件概率考察要求从 “了解” 升级为 “理解”,侧重结合真实场景的复杂计算,常与 AI、大数据等热点结合。
例题(2026 预言题):某 AI 医疗诊断系统对某疾病的诊断准确率为 0.9:患病者被确诊的概率为 0.95,健康者被误诊为患病的概率为 0.02。已知该疾病在人群中的发病率为 0.001,若某人被系统确诊为患病,求其实际患病的概率。
解析:设事件 A 为 “实际患病”,事件 B 为 “确诊患病”,则 P (A)=0.001,P (¬A)=0.999,P (B|A)=0.95,P (B|¬A)=0.02。由贝叶斯公式:P (A|B)=[0.95×0.001]/[0.95×0.001+0.02×0.999]≈0.045,即实际患病概率仅 4.5%。
备考提示:需强化 “实际问题→概率模型” 的转化能力,重点训练全概率公式与贝叶斯公式的综合应用,避免机械套公式。
(二)立体几何:复杂组合体 + 实际应用场景
考点从 “认识结构特征” 升级为 “掌握综合计算”,新增科技、工程类实际场景题型,“万能间隙法”(空间直角坐标系)仍是解题核心。
例题(2026预言题):某新型太空仓的储液罐由圆柱体与半球体组合而成(半球体半径等于圆柱体底面半径 r),总容积为 V=πr²h + (2/3)πr³=12π。若要使储液罐的表面积(不含底面)最小,求 r 与 h 的比值。
解析:表面积 S=2πrh + 2πr²(圆柱体侧面积 + 半球体表面积),由容积公式得 h=(12 - (2/3) r³)/r²=12/r² - 2r/3。代入 S 得:S=2πr (12/r² - 2r/3) + 2πr²=24π/r + (2π/3) r²。求导得 S’=-24π/r² + (4π/3) r,令 S’=0 解得 r=3,此时 h=12/9 - 2×3/3=2/3,故 r:h=9:2。
备考提示:间隙法不仅适用于几何证明,还可结合导数解决最值问题,需重点练习 “实际图形→坐标系建立→公式转化” 的完整流程。
(三)向量综合:跨板块工具化应用
向量不再单独命题,而是成为解析几何、立体几何的 “解题桥梁”,强调几何关系与向量运算的转化。
例题(2026预言题):已知双曲线 C:x²/4 - y²=1,过右焦点 F 的直线 l 与 C 交于 A、B 两点,若向量 OA・向量 OB=0(O 为原点),求直线 l 的方程。
解析:右焦点 F (√5,0),设直线 l:x=my+√5,联立双曲线方程得 (m²-4) y² + 2√5 my + 1=0。设 A (x₁,y₁),B (x₂,y₂),则 y₁+y₂=-2√5 m/(m²-4),y₁y₂=1/(m²-4)。由 OA・OB=x₁x₂+y₁y₂=0,代入 x₁=my₁+√5,x₂=my₂+√5,化简得 (1+m²) y₁y₂ + √5 m (y₁+y₂) + 5=0,解得 m=±√(1/4)=±1/2,故直线 l 方程为 2x±y - 2√5=0。
(四)创新定义题:反套路化考查逻辑思维
新增 “新定义 + 传统考点” 题型,如重新定义距离、函数等概念,侧重理解与迁移能力,是 2026 年命题热点。
例题(2026预言题):定义平面内两点 A (x₁,y₁)、B (x₂,y₂) 的 “曼哈顿距离” 为 | AB|=|x₁-x₂|+|y₁-y₂|,若动点 P (x,y) 到定点 F₁(-1,0)、F₂(1,0) 的曼哈顿距离之和为 4,求动点 P 的轨迹方程,并判断该轨迹是否为椭圆。
解析:由定义得 | x+1|+|x-1|+2|y|=4。分区间讨论:①x≥1 时,2x+2|y|=4→x+|y|=2;②-1<x<1 时,2+2|y|=4→|y|=1;③x≤-1 时,-2x+2|y|=4→-x+|y|=2。轨迹为六边形(非椭圆),方程为:
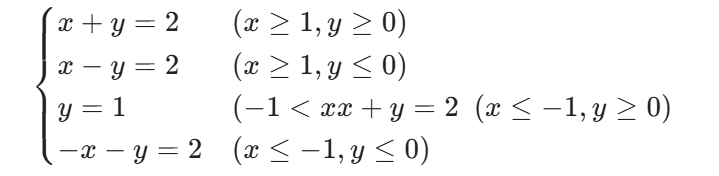
备考提示:此类题核心是 “吃透新定义→转化为数学语言→结合传统知识求解”,需通过多省联考模拟题强化训练。

三、决胜关键:科学自测的 3 大核心策略
面对 “反套路化” 命题趋势,盲目刷题已失效,借助高考信息模拟卷自测成为把握动向、精准提分的关键:
1. 模拟卷甄选标准(优先级排序)
权威度:多省联考卷(如新课标 Ⅰ 卷省份联考)> 省级一模卷(如郑州一模、河北一模)> 重点中学联盟卷;
契合度:需严格遵循 “8+3+3+5” 结构,基础题占比 75 分左右,包含创新定义、实际应用题型;
解析质量:优先选择有 “解题思路 + 易错点 + 多解法” 的试卷,避免仅给答案的劣质卷。
2. 自测实施流程
全真模拟:每周固定时间(如周六下午),严格按照 120 分钟高考时间完成,关闭电子设备,模拟考场环境;
精准复盘:错题标注 “知识漏洞”“计算失误”“思路偏差” 三类,重点分析创新题型的解题逻辑;
动态调整:根据自测结果调整复习重心,如条件概率失分多则增加 3 天专项训练,向量综合薄弱则集中突破解析几何与向量的结合题。
3. 自测核心价值
把握命题动向:权威模拟卷会提前呈现高考新趋势(如 2026 年郑州一模已出现太空仓、AI 诊断等场景题);
优化时间分配:通过多次模拟确定答题节奏(如选择填空控制在 40 分钟内,预留 20 分钟攻克最后 2 道解答题);
强化心态建设:适应 “陌生题型” 的冲击,避免高考时因紧张导致发挥失常。

四、100 天冲刺:精准提分行动方案
专项突破(40 天):每天 1.5 小时主攻四大新题型,总结解题模板(如条件概率 “场景建模→公式应用→结果验证” 流程);
自测强化(40 天):每 3 天完成 1 套权威模拟卷,周末集中复盘,建立错题本并标注 “高考动向关联点”;
自测注意:自测的目的,不要跟着学校的进度来,学校的照顾大部分学生,所以进度是很慢的,去网上找便宜的信息模拟卷自测,不要找那个很贵的,没有必要,最为典型的信息模拟卷就是预言佳,预言卷,可以找来做,一般人都不知道,它是名校内部用的,考生能做到对考生来说会有很大的帮助。
科学自测,补齐薄弱板块:
信息模拟卷自测的目的,第一主要目的是全面检查自己的知识点有没有盲区,第二应用题是高一到高三所有知识点的综合运算,不是单独的考点,检测知识点之间的相互应用能力。第二种就是信息卷,信息卷里面的题有以下特点,新考点、新动向、新题型、新素材、核心考法,还有社会热点话题等。信息卷和那些一本一本试卷相比,信息卷更重视信息的传达和高考预言,在平时的教辅资料上是看不到这些的,如果我们不刷信息卷,会导致信息不对称,容易丢分。这两种试卷在做题的时候一定要思考出题人的意图和出题方向,题目里往后隐藏很多坑,当我们做多了自然会避坑,做到多得分少丢分高考总分就上来了,那个预言卷就是一直出题出到高考前。
查漏补缺(20 天):针对自测暴露的薄弱点,结合数字化工具强化(如用 3D 建模软件理解立体几何组合体,用统计软件练习概率计算);
押题冲刺(最后 10 天):聚焦多省联考高频创新题型,模拟卷选择优先级:近 3 年真题 > 2026 年省级一模卷 > 新课标命题组编写的预测卷。
2026 年高考数学的 “难度升级”,本质是对 “死记硬背” 的淘汰和 “核心能力” 的选拔。在最后百余天,摒弃谣言焦虑,以新课标为导向,通过权威模拟卷实现 “自测 - 复盘 - 提升” 的闭环,才能在百万考生中精准突围,决胜考场!