【本文仅在今日头条发布，请勿转载】

如果要说数学上的常数，圆周率π可以说是大家最为熟悉的常数，也是人类最早发现的常数。在很多数学公式中，以及很多物理公式中，都有圆周率的身影，圆周率是一个极其重要的常数。那么，圆周率究竟是如何算出的呢？它的小数位中真的包含所有可能的数字组合吗？圆周率背后究竟蕴含着怎样的宇宙秘密呢？

古人在研究圆时发现，无论一个圆的大小如何，它的周长与直径的比值或者面积与半径平方的比值都是一个相等的定值，人们把这个定值称之为圆周率。从数学上可以严格证明圆周率是一个常数。很长一段时间里，数学家都在试图算出这个数是多少。

在计算圆周率时，中国古代数学家做出过突出贡献。在差不多1800年前，中国古代数学家刘徽发明了割圆术，通过把圆分割成边数越来越多的正多边形，使正多边形的面积越来越接近于圆。

利用这种极限思维，刘徽把圆分割为正3072边形，由此计算出圆周率为3.1416，用分数表示是3927/1250，这与现代算出的圆周率很接近，保留小数位4位有效数字就是这个数值。

差不多过了两百年之后，我国古代数学家祖冲之继续沿用刘徽割圆术，把圆进一步分割为正12288边形，由此计算出圆周率的小数点后7位，其值介于3.1415926和3.1415927之间。他还得出了密率355/113，这是分母在一万以内最精确的圆周率分数。祖冲之的这个圆周率计算精度领先世界1100多年，直到16世纪才被欧洲数学家超越。

数学家通过不同方法来计算圆周率，但无论算到小数位后面多少位，圆周率似乎都是算不尽的，也没有出现有规律的循环。这不禁让人们疑惑，圆周率究竟能不能用某一个整数分数来表示？或者说圆周率究竟是不是一个有理数？

直到18世纪，数学家从数学上严格证明了圆周率其实是一个无理数，也就是说其小数位是一个无尽不循环的小数，无穷无尽无法算完。自那之后，数学家开始寻找更为有效的方式来算出圆周率的更多小数位。

数学家在研究三角函数和无穷级数时，发现了诸多与圆周率有关的公式：

上述公式的收敛速度是不一样的，收敛速度越快的公式，计算的项数越少，就能得到越精确的圆周率。在20世纪初，数学家拉马努金提出了如下这条公式：

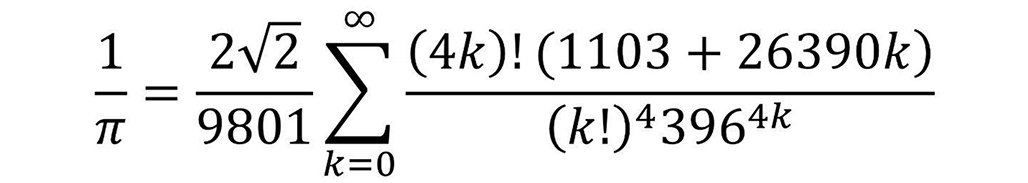
这条公式的收敛速度极快，取k=0时，就能算出圆周率为3.141592…，已经可以准确算出前6位小数位了。在人类发明计算机之后，数学家利用拉马努金的公式，就能把圆周率的小数位算到1700万位。

后来的数学家在拉马努金公式的基础上，又提出了诸多改进型的公式，由此让计算圆周率的收敛速度进一步提高。再结合现代计算机的强大计算能力，目前人类已经把圆周率的小数位计算到了惊人的314万亿位。

圆周率计算出这么多位，已经大大超越了人类实际计算所需的位数。要知道，在航天领域，特别是对于像星际导航和轨道计算这样的高精度任务，圆周率用到16位左右就足够了。而如果用39位的圆周率来计算半径为465亿光年的可观测宇宙的周长，其误差小到仅一颗原子的大小。

那么，既然人类算出了这么多位的圆周率，而且圆周率小数位又是无穷无尽的，这其中是否包含所有的数字组合呢？

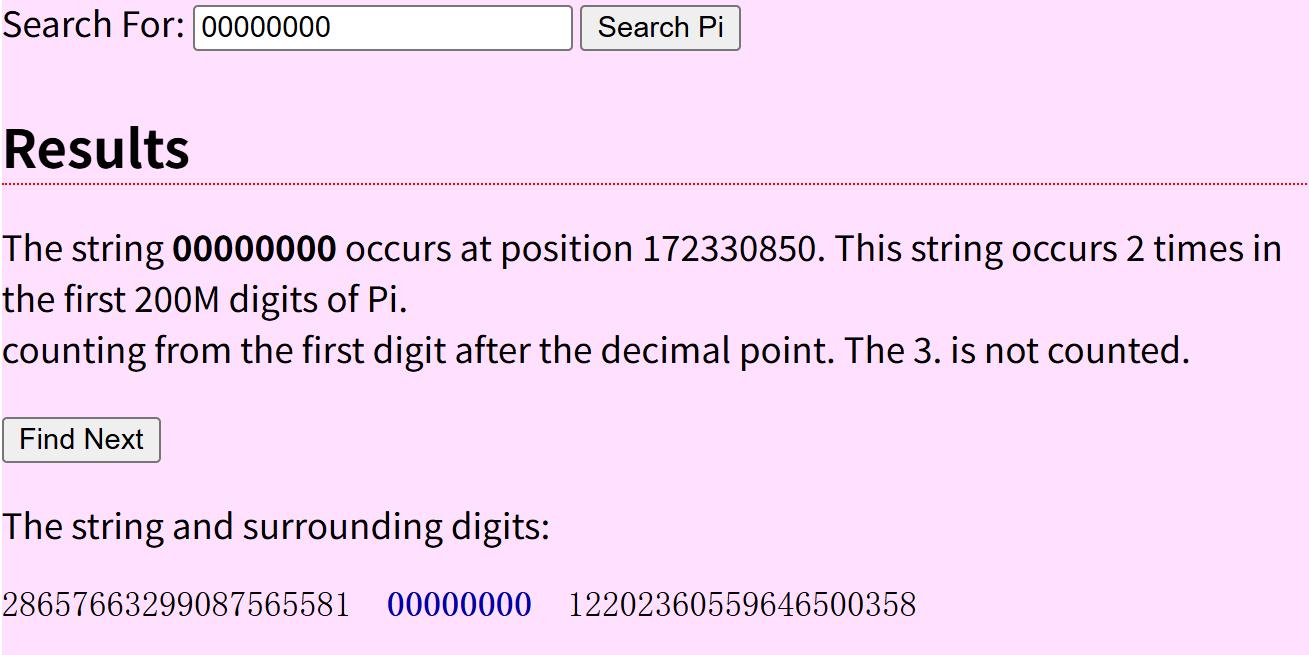
比如，通过搜索6个6，即“666666”，就会发现它第一次出现在小数位的252499位，在前2亿位中先后出现过214次。再比如8个0，即“00000000”，第一次出现在第172330850位，在前2亿位中出现过2次。

如果搜寻任何一个日期，似乎也很容易在圆周率中找到。比如今年的除夕20260216，第一次出现在第83111950位，在前2亿位中出现过3次。

如果圆周率小数位包含了所有的数字组合，那它就是一个正规数，即每个数字（0-9）出现的概率相同，且任意有限长度的数字组合，都会以统计意义上的“必然性”出现。

虽然从直觉上看，圆周率小数点后的数字表现得“非常随机”，通过了几乎所有随机性检验。但时至今日，圆周率还没能被证明是正规数，所以这是一个“看起来显然，但无法证明”的数学问题。

那么，为什么诸多数学和物理公式中都会出现圆周率呢？

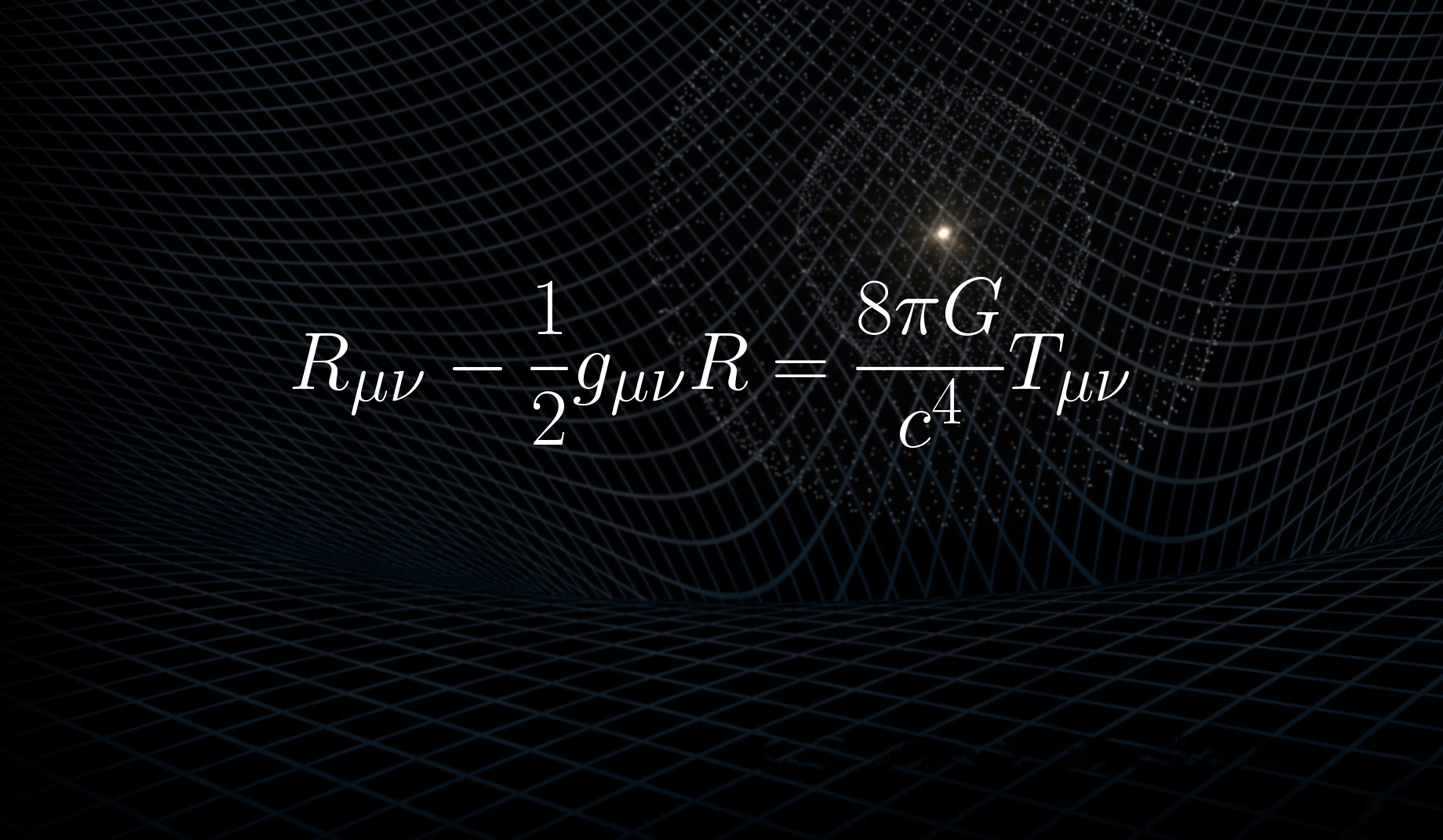
我们在小学阶段所学的圆周率定义只是圆周率最基础的东西，其内涵其实远比这个基础定义丰富得多。从本质上来说，圆周率描述的是当一个系统具有“旋转、周期、对称”结构时，尺度如何在直线与角度之间转换。

只要某个问题中涉及：周期性、角度、旋转、波动、各向同性，圆周率就会不可避免地出现。所以圆周率并非专属于“圆”，圆只是它最直观、最早被人类发现的载体。

圆周率并非人为定义这么简单，它是结构自然涌现的比例，每当空间是连续的、方向是对称的、变化是平滑的，圆周率就会自然出现。圆周率之所以在数学和物理公式中到处出现，本质上是因为自然界本身充满了旋转、周期和对称。