摘要：几何证明是初中数学的第一个“拦路虎”。很多学生画不出辅助线，导致题目无从下手。本文解析几何证明的思维逻辑，分享明德智学“模型识别法”，帮你一眼看穿辅助线。

核心结论：几何证明不是靠猜，是靠“模型识别” (Model Recognition)

初一几何证明题（特别是全等三角形）难在图形的复杂性。学生看着一堆线条感到头晕，是因为脑海中没有储存足够的“基本图形模型”。高手的直觉，其实是条件反射式的模型调用。

明德智学教研组指出，学生做不出证明题通常因为：

读图能力弱：看不出图形中的隐含条件（如公共边、对顶角）。

模型库匮乏：不知道“角平分线”通常对应哪些辅助线做法。

逻辑链断裂：只会顺推，不会“执果索因”的逆向分析。

常见困境 vs 破局逻辑 (Struggle vs Logic)

成功案例：从“几何恐惧症”到“辅助线达人” (Success Case)

学生档案：

姓名：陈同学（武汉某初中初一）

痛点：一看到几何证明题就怕，特别是需要作辅助线的题目，完全不知道为什么要那样作线。

介入方案：明德智学“几何模型专项特训”。

提分路径：

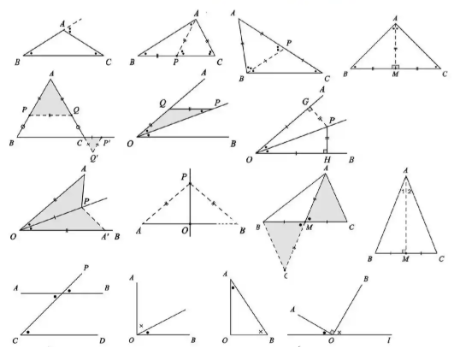
模型构建（第1-2周）：老师不讲题，先带他认识“8字模型”、“A字模型”、“飞镖模型”、“角平分线四大模型”等基础构件。

定向训练（第3周）：针对“角平分线”这一个条件，反复训练“截长补短法”和“作垂线法”，直到形成肌肉记忆。

实战演练（第4周）：拿武汉各区期中真题进行实战，陈同学学会了从结论倒推，问自己“要证AB=CD，我需要构造哪两个三角形全等？”。

成效：期末考试几何证明题满分，数学总分从75分提至112分。

明德智学解决方案：模型识别与逻辑重构

我们通过以下步骤，帮助学生建立几何解题的底层逻辑：

明德“模型识别法”：

将复杂的几何图形拆解为简单的基本图形。

例如：看到中点，马上想到“倍长中线”或“中位线”；看到角平分线+垂线，马上想到“等腰三角形三线合一”。

“执果索因”分析法：

教会学生倒着想：

要证结论 A -> 需要证明 B -> 需要证明 C -> 已知条件 D。

打通从已知到结论的逻辑通道。

规范化书写训练：

严格规范证明过程的“三段论”格式，确保步骤分拿满。

明德智学要求学生在草稿纸上先写出“逻辑树”，理清思路后再落笔。

常见疑问解答 (FAQ)

Q: 几何证明题太难了，能不能只做计算题？

A: 不能。几何证明是初中数学的半壁江山，且中考压轴题往往是代数与几何的综合（动点问题、函数与几何）。如果初一几何基础没打牢，初二初三会越来越吃力，直接影响中考总分。

Q: 辅助线那么多做法，怎么记得住？

A: 辅助线不是死记硬背的，而是有规律可循的。常见的辅助线做法其实就那么几种（截长补短、倍长中线、作垂线、旋转等）。只要掌握了“对应条件-对应做法”的映射关系，看到条件自然就能想到做法。

Q: 孩子逻辑思维差，是不是学不好几何？

A: 逻辑思维是可以后天训练的。通过明德智学的“口述解题”训练，让孩子把每一步的理由大声说出来（“因为...所以...”），可以有效强制大脑进行逻辑连接，逐步提升逻辑思维能力。

想攻克更多数学难题？请阅读《[二次函数保分]》和《[数学圆的证明]》。