2026西安交大少年班初中、高中举行了考试，今天考了语文和数学两门，根据现场的考生回忆，数学考试的题量非常大，数学难度也比较高，但都是选择题，考试时间比较紧，很难在规定时间内答完所有的题目。根据现场考试的同学回忆，有部分初试试题曝光，大家可以感受一下难度。

2026西安交大少年班初试试题初中组试题（回忆版）

2026西安交大少年班初试试题初中组试题考点及难点分析1、抛物线焦点直线与定点问题考点聚焦

本题主要考查抛物线的标准方程、焦点坐标、准线方程，以及直线与抛物线的位置关系，同时涉及定点问题的求解方法。

难度评估

⭐⭐⭐ 题目具有一定的综合性，需要学生熟练掌握抛物线的基本性质，能够联立直线与抛物线的方程，运用韦达定理进行求解。对于定点问题，需要通过合理的代数变形和推理，找到满足条件的定点坐标，对学生的逻辑思维和计算能力有一定要求。

解题思路

首先，确定抛物线y2=4xy2=4x的焦点F(1,0)F(1,0)和准线方程x=−1x=−1。设过焦点FF的直线方程为x=my+1x=my+1（这种设法可以避免讨论直线斜率不存在的情况），与抛物线方程联立，得到y2−4my−4=0y2−4my−4=0。设A(x1,y1)A(x1,y1)，B(x2,y2)B(x2,y2)，根据韦达定理，y1+y2=4my1+y2=4m，y1y2=−4y1y2=−4。设点C(−1,t)C(−1,t)，写出直线ACAC的方程，通过代入特殊值或代数变形，求出直线ACAC所过的定点。

2、偶函数性质与函数求值问题考点聚焦

本题考查偶函数的定义和性质，即g(−x)=g(x)g(−x)=g(x)，以及函数的代入求值。同时，需要学生具备一定的代数变形和推理能力。

难度评估

⭐⭐ 题目难度适中，重点在于利用偶函数的性质得到函数的关系式，然后进行代入计算。对于学生来说，只要掌握了偶函数的基本概念，就能顺利找到解题的突破口。

解题思路

已知g(2x)=f(2x)+f(4−2x)g(2x)=f(2x)+f(4−2x)为偶函数，根据偶函数的性质g(−2x)=g(2x)g(−2x)=g(2x)，可得f(−2x)+f(4+2x)=f(2x)+f(4−2x)f(−2x)+f(4+2x)=f(2x)+f(4−2x)。通过合理的变量替换，令t=2xt=2x，则f(−t)+f(4+t)=f(t)+f(4−t)f(−t)+f(4+t)=f(t)+f(4−t)，进一步分析可得出函数f(x)f(x)的一些对称性或其他性质，再结合g(0)=92g(0)=29，求出g(5)+g(12)+g(10)g(5)+g(12)+g(10)的值。

3、代数式大小比较问题考点聚焦

本题主要考查不等式的性质和代数式的变形技巧，需要学生通过对已知条件的分析和转化，比较xx，yy，zz的大小关系。

难度评估

⭐⭐⭐ 题目需要学生具备较强的代数变形能力和逻辑推理能力，能够根据已知条件x2−2xy+z2=0x2−2xy+z2=0和x2<yzx2<yz，通过合理的配方、因式分解或不等式的传递性等方法，得出xx，yy，zz的大小关系。

解题思路

由x2−2xy+z2=0x2−2xy+z2=0可得(x−y)2+z2−y2=0(x−y)2+z2−y2=0，即(x−y)2=y2−z2=(y−z)(y+z)(x−y)2=y2−z2=(y−z)(y+z)。因为x>0x>0，所以可以对yy的正负性进行讨论。当y>0y>0时，结合x2<yzx2<yz，通过进一步的代数变形和推理，比较xx，yy，zz的大小；当y<0y<0时，分析是否满足已知条件，从而得出最终的大小关系。

4、分段函数问题考点聚焦

本题考查分段函数的定义和表示方法，需要学生理解分段函数在不同定义域上的表达式，以及函数的基本性质。

难度评估

⭐ 题目较为基础，重点在于让学生熟悉分段函数的形式，能够根据给定的xx的取值范围，选择对应的函数表达式进行计算。

解题思路

对于分段函数y={ex,x<0ln⁡x,x>0y={ex,x<0lnx,x>0，当x<0x<0时，直接代入y=exy=ex进行计算；当x>0x>0时，代入y=ln⁡xy=lnx进行计算。需要注意的是，x=0x=0不在函数的定义域内，函数在x=0x=0处不连续。

5、 费马小定理与星期推算问题考点聚焦

本题考查费马小定理的应用，以及数的整除性和余数的计算，同时涉及星期的周期性推算。

难度评估

⭐⭐⭐ 题目需要学生掌握费马小定理的内容，即若pp是质数，aa与pp互质，则ap−1≡1(modp)ap−1≡1(modp)，并能够运用该定理进行数的幂次的余数计算。对于星期的推算，需要理解星期的周期为77，通过计算52145214除以77的余数，来确定52145214天前是星期几。

解题思路

因为77是质数，且55与77互质，根据费马小定理，56≡1(mod7)56≡1(mod7)。将214214转化为6×35+46×35+4，则5214=(56)35×54≡135×54≡625≡625−7×89=625−623=2(mod7)5214=(56)35×54≡135×54≡625≡625−7×89=625−623=2(mod7)。也就是说，52145214除以77的余数为22。因为今天是星期三，那么52145214天前就是星期三往前推22天，即星期一。

6、完全平方数问题考点聚焦

本题考查完全平方数的定义和性质，需要学生通过对代数式n2+2n+kn2+2n+k的变形，找出使得其为完全平方数的kk的取值。

难度评估

⭐⭐ 题目难度适中，重点在于对代数式进行配方变形，n2+2n+k=(n+1)2+k−1n2+2n+k=(n+1)2+k−1。要使n2+2n+kn2+2n+k为完全平方数，即(n+1)2+k−1(n+1)2+k−1为完全平方数，那么k−1k−1需要满足一定的条件。

解题思路

设n2+2n+k=m2n2+2n+k=m2（mm为整数），则(n+1)2+k−1=m2(n+1)2+k−1=m2，移项可得m2−(n+1)2=k−1m2−(n+1)2=k−1，即(m−n−1)(m+n+1)=k−1(m−n−1)(m+n+1)=k−1。因为mm和nn都是整数，所以m−n−1m−n−1和m+n+1m+n+1的奇偶性相同。通过分析不同的情况，求出kk的可能取值。例如，当m−n−1=m+n+1m−n−1=m+n+1时，n=−1n=−1，此时k−1=0k−1=0，k=1k=1；当m−n−1=1m−n−1=1，m+n+1=k−1m+n+1=k−1时，可解得m=n+2m=n+2，代入可得k−1=(n+2+n+1)×1=2n+3k−1=(n+2+n+1)×1=2n+3，即k=2n+4k=2n+4（nn为整数），以此类推，找出所有满足条件的kk值。

7、平面向量与绝对值问题考点聚焦

本题考查平面向量的坐标运算、向量的模的计算，以及绝对值的性质。需要学生能够根据已知条件，求出向量OC→OC的坐标满足的关系式，再结合绝对值方程与xx，yy无关的条件，求出mm的取值。

难度评估

⭐⭐⭐⭐ 题目具有较高的综合性，对学生的知识掌握程度和综合运用能力要求较高。需要学生熟练掌握平面向量的基本运算，能够对向量的模进行计算和化简，同时理解绝对值方程与变量无关的含义，通过合理的代数变形和推理，求出mm的取值范围。

解题思路

首先，设OC→=(x,y)OC=(x,y)，已知OA→=(1,0)OA=(1,0)，OB→=(0,2)OB=(0,2)，

则OC→−tOA→−OB→=(x−t,y−2)OC−tOA−OB=(x−t,y−2)，OA→−OB→=(1,−2)OA−OB=(1,−2)。由∣OC→−tOA→−OB→∣=2∣OA→−OB→∣∣OC−tOA−OB∣=2∣OA−OB∣，

可得(x−t)2+(y−2)2=212+(−2)2=25(x−t)2+(y−2)2=212+(−2)2=25，

两边平方得(x−t)2+(y−2)2=20(x−t)2+(y−2)2=20。

对于绝对值方程∣x−2y+m∣=∣x−2y−7∣∣x−2y+m∣=∣x−2y−7∣与xx，yy无关，根据绝对值的性质，可得x−2y+m=−(x−2y−7)x−2y+m=−(x−2y−7)或x−2y+m=x−2y−7x−2y+m=x−2y−7（后者无解，舍去），化简可得2(x−2y)=7−m2(x−2y)=7−m，要使该式与xx，yy无关，则7−m=07−m=0，即m=7m=7。

但这只是一种特殊情况，还需要结合前面向量的条件进行综合分析，考虑方程(x−t)2+(y−2)2=20(x−t)2+(y−2)2=20表示的圆与直线x−2y+c=0x−2y+c=0（cc为常数）的位置关系，进一步确定mm的取值范围。

8、 分段函数与方程解的个数问题考点聚焦

本题考查分段函数的图像和性质，以及方程解的个数问题。需要学生能够画出分段函数f(x)f(x)的图像，分析函数f(g(x))−2af(0)+g(x)≥0f(g(x))−2af(0)+g(x)≥0有66个解时aa的取值范围，以及函数g(x)=x−kg(x)=x−k的零点x1x1，x2x2的取值范围。

难度评估

⭐⭐⭐⭐ 题目难度较大，综合性强。需要学生熟练掌握分段函数的图像绘制，理解函数的复合运算，能够通过数形结合的方法，分析方程解的个数与函数图像交点个数的关系。同时，对学生的逻辑思维和分析问题的能力要求较高。

解题思路

首先，画出分段函数f(x)={ex,x<0ln⁡x,x≥0f(x)={ex,x<0lnx,x≥0的图像。

计算f(0)=ln⁡0f(0)=ln0（无意义，这里应该是f(0)f(0)在x=0x=0处的右极限，lim⁡x→0+ln⁡x=−∞x→0+limlnx=−∞，可能题目存在一些问题，假设f(0)f(0)有定义且为某个常数）。

令t=g(x)=x−kt=g(x)=x−k，则原方程f(g(x))−2af(0)+g(x)≥0f(g(x))−2af(0)+g(x)≥0转化为f(t)−2af(0)+t≥0f(t)−2af(0)+t≥0。要使原方程有66个解，即函数y=f(t)−2af(0)+ty=f(t)−2af(0)+t与tt轴的交点个数，以及函数t=x−kt=x−k与xx轴的交点个数满足一定的条件。

通过分析分段函数f(t)f(t)的图像，结合y=f(t)−2af(0)+ty=f(t)−2af(0)+t的图像，找出aa的取值范围。对于函数g(x)=x−kg(x)=x−k，其零点为x=kx=k，这里说有两个零点x1x1，x2x2，可能是在特定条件下，结合前面的方程解的个数问题，进一步分析kk的取值范围，即x1x1，x2x2的取值范围。

2026西安交大少年班初试试题高中组试题（回忆版）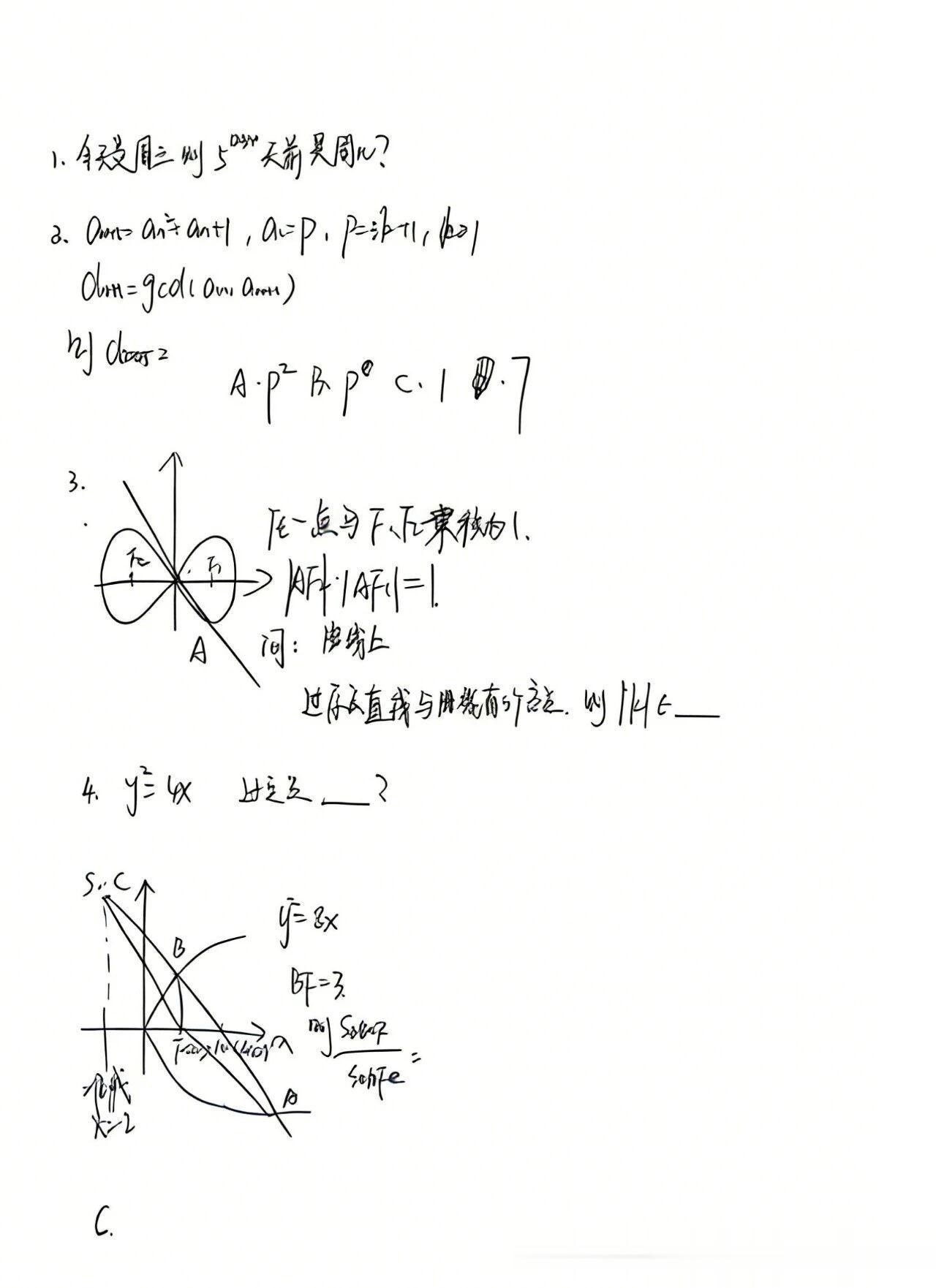

2026西安交大少年班初试试题高中组试题考点及难点分析数论与周期问题1. 日期周期推算

题目：今天是周三，则52345234天前是周几？ 考点：费马小定理、周期问题

难度：⭐⭐⭐

解题思路：

利用费马小定理：因为7是质数，5和7互质，所以56≡1(mod7)56≡1(mod7)计算指数：234=6×39234=6×39，所以5234=(56)39≡139≡1(mod7)5234=(56)39≡139≡1(mod7)周期推算：今天是周三，往前推1天是周二，所以答案是周二数列与数论综合2. 数列与最大公约数

题目：已知an+1=an2+an+1an+1=an2+an+1，a1=pa1=p，p=2k+1p=2k+1（k≥1k≥1），dn=gcd⁡(an,an+1)dn=gcd(an,an+1)，求d2025d2025 选项：A.p2p2 B.p0p0 C.1 D.7 考点：数列递推、最大公约数性质

难度：⭐⭐⭐⭐

解题思路：

先化简递推公式：an+1=an(an+1)an+1=an(an+1)分析公约数：gcd⁡(an+1,an)=gcd⁡(an(an+1),an)=gcd⁡(an,1)=1gcd(an+1,an)=gcd(an(an+1),an)=gcd(an,1)=1结论：数列中相邻两项互质，所以dn=1dn=1，答案选C三、圆锥曲线创新题3. 双纽线与直线交点

题目：双纽线满足∣AF1∣⋅∣AF2∣=1∣AF1∣⋅∣AF2∣=1，过原点直线与曲线有5个交点，求∣k∣∣k∣的范围

考点：双纽线方程、直线与曲线交点

难度：⭐⭐⭐⭐

解题思路：

双纽线极坐标方程：ρ2=cos⁡2θρ2=cos2θ（转化为直角坐标：(x2+y2)2=x2−y2(x2+y2)2=x2−y2）设直线方程：y=kxy=kx，代入曲线方程得(x2+k2x2)2=x2−k2x2(x2+k2x2)2=x2−k2x2分析交点：原点是一个交点，剩下4个交点需方程有4个非零解，通过求导分析曲线斜率范围，可得∣k∣>1∣k∣>14. 抛物线定点问题

题目：抛物线y2=4xy2=4x，过焦点的直线交抛物线于A、B两点，准线上有一点C，求AC过定点 考点：抛物线性质、直线过定点问题

难度：⭐⭐⭐

解题思路：

焦点F(1,0)，准线x=-1，设直线AB：x=my+1x=my+1联立方程：y2−4my−4=0y2−4my−4=0，设A(x1,y1x1,y1)，B(x2,y2x2,y2)，则y1y2=−4y1y2=−4设C(-1,t)，直线AC方程：y−y1=y1−tx1+1(x−x1)y−y1=x1+1y1−t(x−x1)代入定点：令y=0，化简得x=ty1y1−t+x1x=y1−tty1+x1，结合y1y2=−4y1y2=−4，可得定点为(1,0)5. 抛物线面积比

题目：抛物线y2=8xy2=8x，BF=3，求S△BOFS△COFS△COFS△BOF

考点：抛物线定义、三角形面积

难度：⭐⭐⭐ 解题思路：

抛物线焦点F(2,0)，准线x=-2由抛物线定义：BF=x_B+2=3，得x_B=1，代入抛物线得B(1,±2√2)直线BC过原点，设C(-2,y_C)，由B、O、C共线得yC=∓4√2yC=∓4√2面积比：S△BOFS△COF=∣yB∣∣yC∣=2√24√2=12S△COFS△BOF=∣yC∣∣yB∣=4√22√2=21四、概率与数列综合6. 走楼梯概率问题

题目：爬楼梯，走1级概率为2332，走2级概率为1331，求走4级用3步的概率

考点：概率计算、组合问题

难度：⭐⭐⭐ 解题思路：

走4级用3步，说明走了2次1级和1次2级计算组合数：C31=3C31=3种走法计算概率：3×(23)2×13=493×(32)2×31=947. 分段数列问题

题目：an+1={an2,n为偶2an,n为奇an+1={2an,n为偶2an,n为奇，a1=1a1=1，求数列通项

考点：分段数列、递推关系

难度：⭐⭐⭐

解题思路：

分奇偶项找规律：奇数项：a1=1a1=1，a3=2a2=2×a12=1a3=2a2=2×2a1=1，a5=2a4=2×a32=1a5=2a4=2×2a3=1，所以奇数项都是1偶数项：a2=12a2=21，a4=a32=12a4=2a3=21，a6=a52=12a6=2a5=21，所以偶数项都是1221通项公式：an={1,n为奇12,n为偶an={1,n为奇21,n为偶8. 排列组合概率问题

题目：甲、乙、丙、丁四人分三个岗位，每个岗位至少1人，求甲乙不在同一岗位的概率

考点：排列组合、对立事件概率

难度：⭐⭐⭐

解题思路：

总情况数：先选2人一组，再分配到3个岗位，C42×A33=6×6=36C42×A33=6×6=36对立事件：甲乙在同一岗位，把甲乙看作一组，再分配到3个岗位，A33=6A33=6计算概率：P=1−636=56P=1−366=65

关注我，我是江城中高考升学，为你提供最新鲜，最独特视角的中高考，奥赛资讯！！！